3D 世界中坐标变换流程,以及 Three 中相关的内容,至于数学部分,比如矩阵与向量等,这里不重点铺开,在另外的数学篇铺开。
为什么需要矩阵
为什么需要矩阵
- 理论上讲我们的确可以只通过数学公式就能实现变换,但实际的情况却是在变换十分复杂时,直接使用数学表达式来进行运算也是相当繁复的
- 在现实中常常使用矩阵(由 m×n 个标量组成的长方形数组)来表示诸如平移、旋转以及缩放等线性变换
- 矩阵的乘积 = 映射的合成
- 逆矩阵 = 逆映射
向量基础
向量:具有大小和方向,由于向量表示的是方向,起始于何处并不会改变它的值。数学家喜欢在字母上面加一横表示向量。当用作公式时,常用矩阵表示
标量:Scalar,THREE Vector3 的 api 中很多与 Scalar 相关的函数,就是与标量进行运算的意思
由于向量是一个方向,所以有些时候会很难形象地将它们用位置(Position)表示出来。为了让其更为直观,我们通常设定这个方向的原点为(0, 0, 0),然后指向一个方向,对应一个点,使其变为位置向量(Position Vector)
向量取反:一个向量的每个分量前加负号就可以实现取反了(或者说用 -1 数乘该向量)
向量加减
- 加:向量的加法可以被定义为是分量的(Component-wise)相加,即将一个向量中的每一个分量加上另一个向量的对应分量
- 减:像普通数字的加减一样,向量的减法等于加上第二个向量的相反向量。两个向量的相减会得到这两个向量指向位置的差。这在我们想要获取两点的差会非常有用。
向量的模(长度):n维向量的各个分量的平方和再开方,在三维中表示向量的空间长度。常用 ||v|| 或 |v| 表示。
单位向量(Unit Vector):单位向量有一个特别的性质——它的长度是 1。我们可以用任意向量的每个分量除以向量的长度得到它的单位向量。通常单位向量会变得很有用,特别是在我们只关心方向不关心长度的时候(如果改变向量的长度,它的方向并不会改变)
向量点乘
- 几何意义:向量 a 在向量 b 方向上的投影与向量 b 的模的乘积,因此等于它们的数乘结果乘以两个向量之间夹角的余弦值
a·b=|a||b|·cosθ - 夹角 θ 很有用,因为当 a 和 b 均为单位向量时,表达式也就直接变成了 cosθ,因此
- 90 度的余弦角是 0,因此点乘能够测试出两个向量是否正交
- 0 度的余弦角是 1,因此点乘能够用来测试两个向量是否平行
- 反过来看,也可以通过点乘的结果计算两个非单位向量的夹角,点乘的结果除以两个向量的长度之积,得到的结果就是夹角的余弦值
- Dot Product:点乘是通过将对应分量逐个相乘,然后再把所得积相加来计算的,若
a=(x1,y1),b=(x2,y2),则a·b=x1·x2+y1·y2
向量叉乘
- Cross Product:叉乘只在 3D 空间中有定义,它需要两个不平行向量作为输入,生成一个正交于两个输入向量的第三个向量
- 几何意义:c 是垂直 a、b 所在平面,且以
|b|·sinθ为高、|a|为底的平行四边形的面积 - 若坐标系是满足右手定则的,当右手的四指从 a 以不超过 180 度的转角转向 b 时,竖起的大拇指指向是 c 的方向
- 不同于其他运算,如果你没有钻研过线性代数,可能会觉得叉乘很反直觉,暂时直接记住公式即可(需要通过行列式去理解)
矩阵基础
矩阵的相关运算
- 矩阵与标量之间的加减:矩阵每个元素均加减变量
- 矩阵之间的加减:两个矩阵对应元素的加减运算,因此加法和减法只对同维度的矩阵才是有定义的
- 矩阵的数乘:和矩阵与标量的加减一样,矩阵与标量之间的乘法也是矩阵的每一个元素分别乘以该标量
- 矩阵相乘
- 只有当左侧矩阵的列数与右侧矩阵的行数相等,两个矩阵才能相乘。矩阵的乘法是一系列乘法和加法组合的结果,它使用到了左侧矩阵的行和右侧矩阵的列。矩阵相乘是左边矩阵行乘右边矩阵的列
- 矩阵相乘不遵守交换律(Commutative),也就是说A⋅B ≠ B⋅A。
- 矩阵与向量相乘
- 向量:它其实就是一个 N×1 矩阵,N 表示向量分量的个数
- 矩阵和向量的乘法很关键:因为很多有趣的 2D/3D 变换都可以放在一个矩阵中,用这个矩阵乘以我们的向量将变换(Transform)这个向量。
- 单位矩阵
- Identity Matrix
- 单位矩阵是一个除了对角线以外都是 0 的 N×N 矩阵。
- 单位矩阵和向量相乘,不会改变原向量
- 齐次坐标
- 向量的 w 分量也叫齐次坐标。想要从齐次向量得到 3D 向量,我们可以把 x、y 和 z 坐标分别除以 w 坐标。我们通常不会注意这个问题,因为 w 分量通常是 1.0。
- 使用齐次坐标有几点好处
- 它允许我们在 3D 向量上进行位移(如果没有 w 分量我们是不能位移向量的)
- 如果一个向量的齐次坐标是 0,这个坐标就是方向向量(Direction Vector),因为 w 坐标是 0,这个向量就不能位移
矩阵组合
- 使用矩阵进行变换的真正力量在于,根据矩阵之间的乘法,我们可以把多个变换组合到一个矩阵中。
- 矩阵乘法是不遵守交换律的,这意味着它们的顺序很重要。
- 当矩阵相乘时,在最右边的矩阵是第一个与向量相乘的,所以你应该从右向左读这个乘法。
- 建议您在组合矩阵时,先进行缩放操作,然后是旋转,最后才是位移,否则它们会(消极地)互相影响。
逆矩阵
- A 点通过矩阵转换到 B,B 可通过逆矩阵还原到 A
- 逆矩阵与原矩阵相乘等于单位矩阵,任何矩阵乘以单位矩阵的结果都是其本身,可用于实现矩阵的除法
- 计算逻辑比较复杂,正儿八经的计算需要理解线性代数中的行列式,这里就不展开
对称矩阵:以主对角线为对称轴,各元素对应相等的矩阵,对称矩阵是一个方形矩阵,其转置矩阵和自身相等
矩阵与向量乘法简单表达
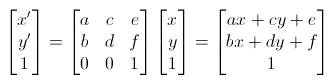
3D 世界中常见矩阵
这里引用目前工作用到一个 oda 库中的一些参数名词,其他库也是类似的
在解释左边变换之前,先需要知道 3D 世界中重要得 5 个坐标系统
- 局部空间(Local Space,或称为物体空间(Object Space)):3D 模型的坐标,定义了 3D 模型本身的顶点空间
- 世界空间(World Space):想象中的 3D 世界,没有考虑任何视角
- 观察空间(View Space,或称为眼空间(Eye Space)):从摄像机的视角所观察到的空间,和具体的 viewParams 密切相关
- 裁剪空间(Clip Space):判断哪些顶点显示在屏幕上,也和具体的 viewParams 密切相关
- 屏幕空间(Screen Space)
viewParams 的 up、target、position 确定视图矩阵。viewFieldWidth、viewFieldHeight、perspective 确定投影矩阵,在 THREE.JS 中就表现为创建 Camera 时的参数了
为了将坐标从一个坐标系变换到另一个坐标系,我们需要用到几个变换矩阵,最重要的几个分别是模型(Model)矩阵、观察(View)矩阵和投影(Projection)矩阵。
- 模型矩阵(Model Matrix):用于将物体的坐标从局部变换到世界空间。
- 观察矩阵(View Matrix):用来将世界坐标变换到观察空间,观察空间是将世界空间坐标转化为用户视野前方的坐标而产生的结果。因此观察空间就是从摄像机的视角所观察到的空间。
- 投影矩阵(Projection Matrix):将顶点坐标从观察变换到裁剪空间,它指定了一个范围的坐标,比如在每个维度上的 -1000 到 1000。投影矩阵接着会将在这个指定的范围内的坐标变换为标准化设备坐标的范围 (-1.0, 1.0)。所有在范围外的坐标不会被映射到在 -1.0 到 1.0 的范围之间,所以会被裁剪掉。
整个变换流程
- 局部坐标是对象相对于局部原点的坐标,也是物体起始的坐标。
- 下一步是将局部坐标变换为世界空间坐标,世界空间坐标是处于一个更大的空间范围的。这些坐标相对于世界的全局原点,它们会和其它物体一起相对于世界的原点进行摆放。
- 接下来我们将世界坐标变换为观察空间坐标,使得每个坐标都是从摄像机或者说观察者的角度进行观察的。
- 坐标到达观察空间之后,我们需要将其投影到裁剪坐标。裁剪坐标会被处理至 -1.0 到 1.0 的范围内,并判断哪些顶点将会出现在屏幕上。
- 最后,我们将裁剪坐标变换为屏幕坐标,我们将使用一个叫做视口变换(Viewport Transform)的过程。视口变换将位于 -1.0 到 1.0 范围的坐标变换到由 glViewport 函数所定义的坐标范围内。
找了三张图用于表示整个变换流程,自行看那个好理解吧 图一

图二
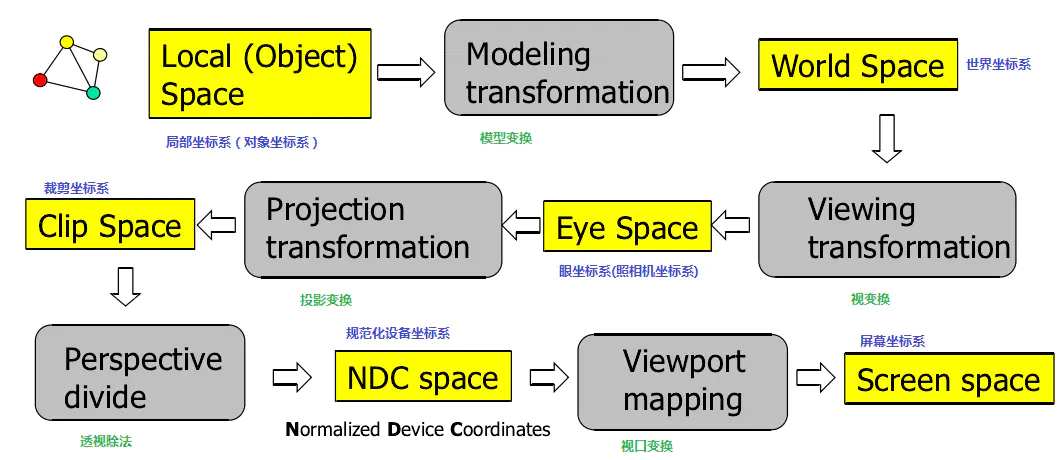
图三
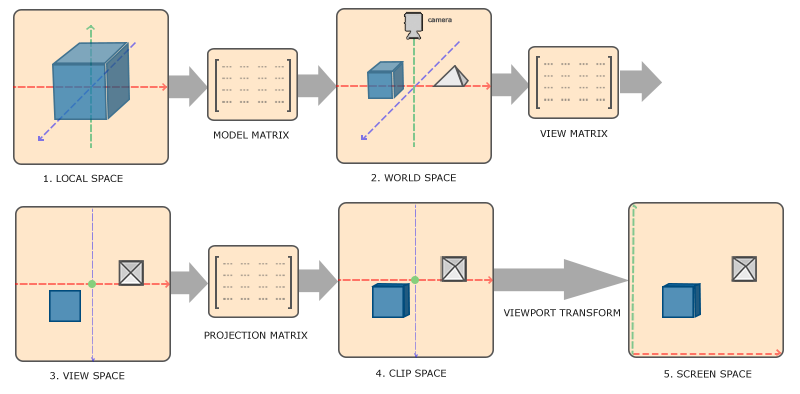
之所以将顶点变换到各个不同的空间的原因是有些操作在特定的坐标系统中才有意义且更方便。
- 当需要对物体进行修改的时候,在局部空间中来操作会更说得通;
- 如果要对一个物体做出一个相对于其它物体位置的操作时,在世界坐标系中来做这个才更说得通;
将特定范围内的坐标转化到标准化设备坐标系的过程(而且它很容易被映射到 2D 观察空间坐标)被称之为投影(Projection),因为使用投影矩阵能将 3D 坐标投影(Project)到很容易映射到 2D 的标准化设备坐标系中。
ODA 中名词
常用矩阵
- view.projectionMatrix:投影矩阵
- view.worldToDeviceMatrix:世界坐标转屏幕坐标
- view.eyeToWorldMatrix:视图矩阵的逆矩阵,用于将视图坐标转回世界坐标
- view.viewingMatrix:视图矩阵,用于将世界坐标转视图坐标
在提供了相关矩阵了基础上,也提供了更易懂的函数
- viewer.toEyeToWorld(x, y, z):视角坐标转世界坐标
- viewer.screenToWorld(x, y):屏幕坐标转世界坐标
- point3d.transformBy(matrix):应用矩阵变换
- viewer.getTransform(from, to):获取映射矩阵
视角参数 viewParams
- viewPosition
- viewTarget
- upVector
- viewFieldWidth
- viewFieldHeight
- perspective:是否透视
形象的理解 Camera 的 upVector 属性:好比你的眼睛就是镜头,焦点就是 lookAt,你头顶就是 up 正方形方向
相关矩阵变换的验证:世界坐标到设备坐标的转换
// 假定设备的宽高为 1000 * 610
var a = lib.Point3d.createFromArray([1,1,0]);
// 直接通过框架封装好的矩阵直接一步到位
a.transformBy(viewer.activeView.worldToDeviceMatrix); // [458.2600819854454, 159.3051914642516, 0.5]
// 按照顺序一步步验证
var b = lib.Point3d.createFromArray([1,1,0]);
// 世界坐标 => 视角坐标 => 投影坐标,记住这里是左乘
b.transformBy(viewer.activeView.viewingMatrix.preMultBy(viewer.activeView.projectionMatrix)); // [0.4582600819854455, 0.7388439484192596, 0.5]
// 转 NDC 坐标 x = [-1, 1] y = [-1, 1] 下面的目的是将 [0, 1] 的范围扩展到 [-1, 1]
// Xn = 0.4582600819854455 * 2 - 1 = -0.08347983602910902
// 转设备坐标
// -0.08347983602910902 * 1000 / 2 + 1000 / 2 === 直接通过 worldToDeviceMatrix 直接获取的值
// Yn = 0.7388439484192596 * 2 - 1 = 0.4776878968385192
// 转设备坐标
// 0.4776878968385192 * -610 / 2 + 305 = 159.30519146425164
Three.js 中的矩阵
为什么 Three.js 使用 4*4 矩阵
- 使用 3*3 矩阵可以搞定旋转变换,但却解决不了平移问题
- 因为平移表达式中带有一个常量,没有办法使用
3*3的矩阵来表示平移。解决办法就是使用4*4矩阵实现,随之而来的问题就是如何让三维坐标和 4*4 矩阵相乘呢 - 为了解决三维矢量和 4*4 矩阵相乘的问题,我们为三维矢量添加了第四个分量,这样之前的三维矢量 (x,y,z) 就变成了四维的 (x,y,z,w),这样由 4 个分量组成的矢量便被称为齐次坐标。需要说明的是,齐次坐标 (x,y,z,w) 等价于三维坐标 (x/w,y/w,z/w),因此只要 w 分量的值是 1,那么这个齐次坐标就可以被当作三维坐标来使用,而且所表示的坐标就是以 x,y,z 这 3 个值为坐标值的点。
在 ThreeJS 中,矩阵是以列主序的方式存储的。也就是说通过数组绘制矩阵时,需要竖向书写。
THREE 中定义了下述三个矩阵:
- 相机投影类型:投影矩阵(ProjectMatrix),通过
camera.projectionMatrix获得 - 相机的位置和方向:视图矩阵 (CameraMatrixWorldInverse 或 ViewMatrix),通过
camera.matrixWorldInverse获得,注意,camera.matrixWorld是相机在三维空间中的位置矩阵,不要搞混啦 - 物体的位置和形变:物体位置矩阵(ObjectWorldMatrix),通过
object.matrixWorld获得,注意,THREE 中的物体是有层级关系的,所以 THREE 中物体的matrixWorld是通过 local matrix(object.matrix)与父亲的matrixWorld递归相乘得到的
三维投影矩阵计算公式如下
// 乘以该矩阵后得到了标准设备坐标,注意从右往左看
const uMatrix = ProjectMatrix * CameraMatrixWorldInverse * ObjectMatrixWorld
我们可以通过矩阵运算推导出视图矩阵(非常重要且有趣)
const eye = new THREE.Vector3(0, 0, 100);
const up = new THREE.Vector3(0, 1, 0);
const at = new THREE.Vector3(1, 2, 3);
const N = new THREE.Vector3();
N.subVectors(eye, at);
N.normalize();
const U = new THREE.Vector3();
U.crossVectors(up, N);
U.normalize();
const V = new THREE.Vector3();
V.crossVectors(N, U);
V.normalize();
const R = new THREE.Matrix4();
R.set(U.x, U.y, U.z, 0,
V.x, V.y, V.z, 0,
N.x, N.y, N.z, 0,
0, 0, 0, 1);
const T = new THREE.Matrix4();
T.set(1, 0, 0, -eye.x,
0, 1, 0, -eye.y,
0, 0, 1, -eye.z,
0, 0, 0, 1);
const V = new THREE.Matrix4();
V.multiplyMatrices(R, T);
console.log(V);
屏幕坐标与世界坐标互转
世界坐标转换为屏幕坐标
- 调用 Vector3 的 project 函数,传入 camera,返回设备标准坐标
- 设备标准坐标转屏幕坐标
屏幕坐标转世界坐标
- 屏幕坐标转设备标准坐标
- 调用 Vector3 的 unproject 函数,传入 camera,得到世界坐标
假设 canvas 中有一点 (x,y),这个点在空间坐标系中为 (x1,y1),那么这个转换公式是:
var x1 = (x / w) * 2 - 1
var y1 = -(y / h) * 2 + 1
有了 ndc 坐标后,转换为世界坐标就比较简单了,three 还很友好的给我们封装了方法,后面我们会了解到 unproject 的源码实现
const worldVector = stdVector.unproject(camera);
世界坐标转屏幕坐标
- 通过 Vector3对象的方法 project(camera),返回的结果是世界坐标 worldVector 在 camera 相机对象矩阵变化下对应的标准设备坐标,标准设备坐标 xyz 的范围是
[-1,1]。 - 计算 canvas 中心点坐标,做简单计算即可
具体代码如下
// 假定画布满屏
const centerX = window.innerWidth / 2;
const centerY = window.innerHeight / 2;
const standardVec = worldVector.project(camera);
const screenX = Math.round(centerX * standardVec.x + centerX);
const screenY = Math.round(-centerY * standardVec.y + centerY);
Vector3
Three.js 中 Vector3 相关函数,几个重要或不好理解的记录一下
- applyEuler(euler: Euler):通过将 Euler(欧拉)对象转换为 Quaternion(四元数)并应用,将欧拉变换应用到这一向量上。
- applyAxisAngle(axis: Vector3, angle: number):将轴和角度所指定的旋转应用到该向量上。同样是将旋转应用到 Vector3 上。
- applyMatrix3(m: Matrix3)
- applyMatrix4(m: Matrix4)
- applyQuaternion(q: Quaternion)
- project(camera: Camera):使用所传入的摄像机来投影(projects)该向量。
//three.js源码为 new THREE.Vector3().applyMatrix4(camera.matrixWorldInverse).applyMatrix4(camera.projectionMatrix); - unproject(camera: Camera):使用所传入的摄像机来反投影(projects)该向量
//three.js源码为 new THREE.Vector3().applyMatrix4(camera.projectionMatrixInverse).applyMatrix4(camera.matrixWorld); - clamp(min: Vector3, max: Vector3):clamp 系列用于限制最大最小值
- negate():向量取反
- dot(v: Vector3):点积
- normalize():转为单位向量
- cross(a: Vector3, w?: Vector3):叉积
- angleTo(v: Vector3)
- distanceTo(v: Vector3)
- distanceToSquared(v: Vector3):计算该向量到传入的 v 的平方距离。 如果你只是将该距离和另一个距离进行比较,则应当比较的是距离的平方, 因为它的计算效率会更高一些。因为开方比较耗时
Matrix3 方法
- setFromMatrix4(m: Matrix4)
- getInverse(matrix: Matrix3, throwOnDegenerate?: boolean): Matrix3
- 求传入矩阵m的逆矩阵,使用解析法将该矩阵设置为传递矩阵 m 的逆矩阵。
- 行列式为零的矩阵不能求逆。如果尝试这样做,该方法将返回一个零矩阵。
- multiply(m: Matrix3)
- premultiply(m: Matrix3): Matrix3
欧拉角与四元素
欧拉角:Euler(x, y, z, order),x/y/z 分别表示在对应轴上的旋转量,用弧度表示。order 表示顺序,默认为 XYZ。
欧拉角存在万向锁问题:当三个万向节其中两个的轴发生重合时,会失去一个自由度的情形。
四元数的出现就可以解决欧拉角的万向锁问题和万向锁带来的插值不是线性的问题。同时比起三维正交矩阵表示,四元数表示能够更方便地给出旋转的转轴与旋转角。更安全,而且计算会更有效率。
讲解四元素的资料